Intro
I’ve been working on this off and on for awhile. Simulator is a Ruby gem which provides functionality for creating discrete time models, and running those models. You can find the Homepage for the Simulator gem on Github.
Take the following two examples included with the gem.
Ball Drop
Let’s say we want to model a ball that is dropped. Assuming I’m not modeling any bounces, I just need to show the affect of acceleration due to gravity on the position of the ball in space. Position is a function of velocity, which is a function of acceleration. We can model this system using the gem thusly.
# We create a model that simulates a ball drop
model = Simulator::Model.new do
name = "Ball drop model"
# create a couple static variables to represent
# acceleration with default values
var :ax, 0
var :ay, - 9.8
# create dynamic variables bound to some
# computation, with default values.
# velocity is affected by acceleration
eqtn(:vx, 20) { vx + ax }
eqtn(:vy, 50) { vy + ay }
# position is affected by velocity
eqtn(:x, 10) { x + vx }
eqtn(:y, 100) { y + vy }
end
There is a simple DSL provided that makes creating the models easier.
Hopefully it’s easy enough to follow. We initialize two static
variables, ax and ay, which are set to 0 and -9.8, respectively
(acceleration due to gravity is equal to -9.8m/s\^2.)
Next, we create two “equations”. These are just dynamic variables,
variables that depend on the values of other variables, or on some sort
of computation. Note that we just pass regular ruby blocks to the eqtn
method. These could really perform any ruby code. The result of the
block gets stored in the variable given as a symbol. So, we state that
the variable vy is dependent on a the addition of vy + ay. vy + ay will
be the sum of the values vy and ay from the previous period. We do the
same for vx.
Finally, the position of the ball, the coordinates x and y, depend on the velocity. We also set the default initial position of (10, 100).
Next, we create a “run” of the model, and step it 10 periods. This would be the equivalent of 10 seconds (because of what we set acceleration to).
model_run = model.new_run
model_run.step 10
Note that although we do not do so here, we could alter the values of run variables in each period, like so:
model_run.set ax: 5
model_run.step
This would give the ball an acceleration in the x direction, and this value would be propagated through subsequent periods (because the variable is static).
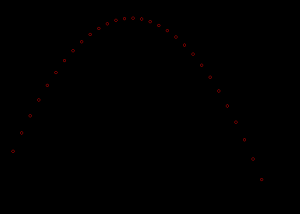
Once we have stepped the run, we can request the series data in case we want to plot it. We can retrieve and plot the data like so:
xs, ys = model_run.data.series :x, :y
require 'chunky_png'
image = ChunkyPNG::Image.new @width, @height,
ChunkyPNG::Color::BLACK
pts.each do |pt|
x, y = pt
# flip y due to inverted coordinate system
y = @height - y
image.circle x, y, 3, ChunkyPNG::Color('red')
end
image.save filename
and we’d get something like this:
Mortgages
A mortgage involves a balance, loan payment, and interest rate. Let’s create a model for that.
model = Model.new do
name = "Mortgage model"
# monthly steps
var :base_rate, 0.08
eqtn(:annual_rate) { base_rate }
eqtn(:monthly_rate) { annual_rate / 12.0 }
var :payment, 2000
eqtn :balance, 250000 do
balance * (1 + monthly_rate) - payment
end
end
We want the period to be monthly instead of annually, so note the
monthly_rate variable above. We also have various default values we
will override in a bit. Let’s look at 3 types of mortgages, fixed,
balloon, and variable. Fixed rate mortgages have a constant interest
rate locked over a defined term (such as 30 years). Let’s see what
happens to the balance at the end of 30 years for each of these loan
types. A balloon loan has a lower monthly payment, but a large payment
at the end of the term. A variable loan has a term where the interest
rate is indexed to a published interest rate, and then a period where
the rate is fixed. Below, we simplify things by assuming that we will
just pay different amounts for each of the terms.
fixed = @model.new_run
fixed.set payment: 2100
fixed.step 30*12
# balloon
balloon = @model.new_run
balloon.set payment: 1850
balloon.step 30*12
variable = @model.new_run
# first 10 years, stick with low payment
variable.set payment: 1800
variable.step 10*12
# subsequent years, balloon to higher payment
# until its paid
variable.set payment: 2100
variable.step 20*12
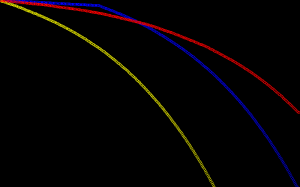
And then we can get the series data and plot it similarly to before. It results in an image like the one below.
- Fixed = yellow
- Variable = blue
- Balloon = red
You can find the homepage for the Simulator gem on Github and find the gem on RubyGems.